Utilizando numpy, realiza los siguientes ejercicios:
1 Crea un arreglo de números aleatorios entre 3 y 5, cuya forma sea de 10x8x2
2 Utiliza booleanos como índices para imprimir los números del arreglo cuyo valor sea mayor que 4.7
3 Encuentra el valor promedio del arreglo, calculado sobre la 3era dimensión (debes obtener 80 números)In [2]:
# Aquí tus respuestas
# 1
# 2
# 3
Utiliza pandas, matplotlib, y cualquier otro módulo que consideres necesario para realizar los siguientes ejercicios:
1.- Lee el archivo Top_secret.csv y guárdalo en un DataFrame, manteniendo sólo las columnas marcadas con los nombres STATUS, Data_value, UNITS, MAGNTUDE y Period
2.- A todos los elementos obtenidos de la columna "Data_value", súmale un número aleatorio entre 0 y 100.
3.- Aplica el método de mínimos cuadrados para ajustar una recta a dichos datos (x es "Period" e y es "Data_value" modificado, es decir, después del paso anterior).
4.- Utiliza matplotlib para graficar los datos originales y la recta que encontraste para verificar que buscar una aproximación lineal es razonable en este caso. Tu gráfica debería tener etiquetas para las dos curvas, título en los ejes x e y, y un título general para la gráfica. In [ ]:
# Aquí tus respuestas
# 1
# 2
# 3
# 4
Utilizando numpy y matplotlib, realiza los siguientes ejercicios:
1 Utiliza numpy para cargar el archivo de datos "Figura_geometrica.dat" y grafica con puntos verdes las 200 parejas de puntos que contiene el archivo.
2 Crea una función que, sin utilizar ciclos, te permita desplazar sumar un vector arbitrario al conjunto de puntos que recién cargaste.
3 Utiliza tu función para desplazar el cuadrado original que obtuviste de "Figura_geometrica.dat", en 1.5 unidades en x y en 3.2 unidades en y. Grafica la nueva figura. Observa la imagen en donde se representa el resultado esperado (puntos negros representan la figura original y los rojos la figura desplazada con la función). 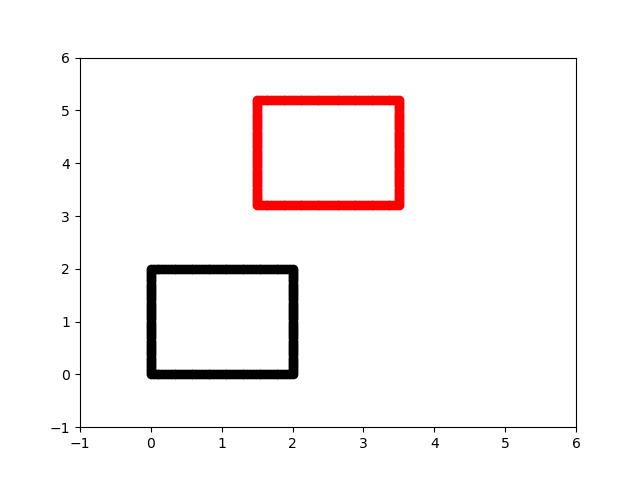
In [3]:
# Aquí tus respuestas
# 1
# 2
# 3
In [ ]:

